Dear Jakob and SUMO team,
Thank you very much for the answer.
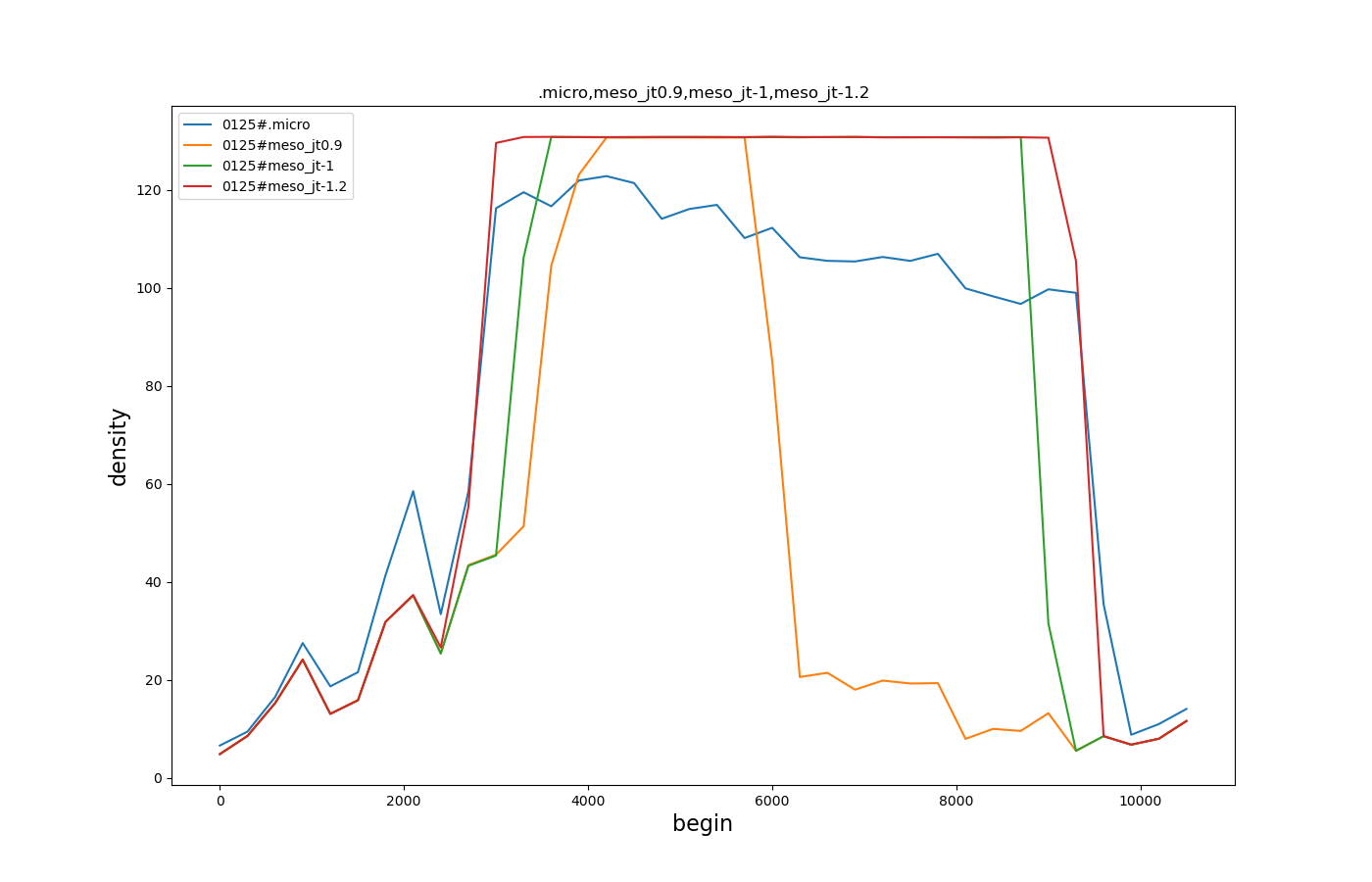
Yes, I see the influence of the jam threshold value now although in my simulation the density evolution after changing it to -1 (see below) is quite different from the plot you showed me.
The flat density in the jam state indeed means that the propagating space is actually not considered.
Then the remaining question I would like to ask is that whether the definition of this jam threshold occupancy is the same as the logic of the critical density on a fundamental diagram.
Thanks a lot!
Best regards,
Ying-Chuan
From: Jakob Erdmann <namdre.sumo@xxxxxxxxx>
Sent: Wednesday, April 2, 2025 5:21 PM
To: Sumo project User discussions <sumo-user@xxxxxxxxxxx>
Cc: Ni Ying-Chuan <ying-chuan.ni@xxxxxxxxxxxxxxxx>
Subject: Re: [sumo-user] The mesoscopic model
Your concern may be valid insofar the current algorithm possibly overestimates void space propagation (especially on short edges).
However, the mismatch between microscopic and mesoscopic behavior is mainly caused by an unfortunate choice of the parameter meso-jam-threshold 0.9
With this setting, the meso model almost never enters the jammed state.
The default values from Eissfeldts dissertation was set to 0.29 (calibrated for motorways). This is unsuitable for road networks with a wide range of speed limits.
The default works much better than 0.9 and an even better fit is reached with -1.2
For clarity, the plot only shows the most upstream edge which also showed the highest discrepancy.
Note, that the lower maximum density in sumo is an artifact of the insertion rules: there are no half cars and in micro, the next car can only enter if a full gap has traveled to the start of the edge. In contrast, meso cars are inserted
as soon as the total space on an edge permits it.
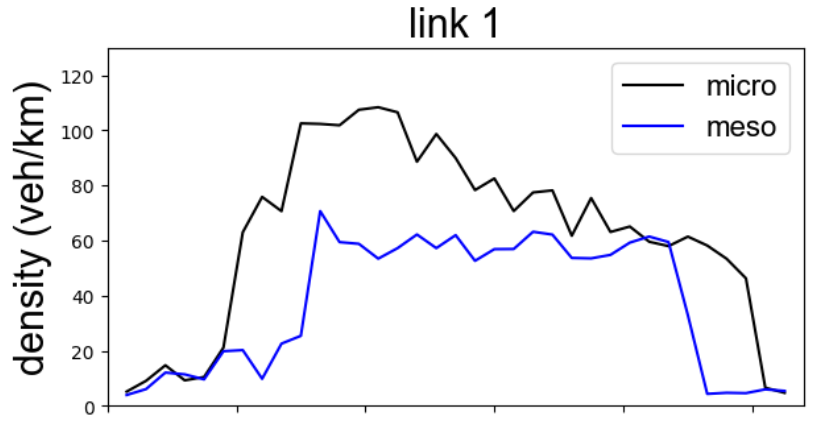
I would like to test the accuracy of the mesoscopic model in SUMO, which is based on the Eissfeldt's dissertation (2004).
The model describes that when there is a spillback (the downstream edge is completely occupied), the headway from upstream edge to the
downstream edge is the time required for a space to travel upstream, which is of course theoretically correct.
However, in the case I implemented, it seems that the headway is immediately updated in the following time steps when a vehicle leaves
the downstream link (the link becomes free because of the smaller number of vehicles), while the void space hasn't yet arrived at the upstream end actually.
The resulting link density evolutions are hence very different from the microsimulation ground-truth. The congestion ends earlier because
spillback is not properly considered.
Attached are the case study of a simple urban corridor.
Could you let me know if this is a problem that was overlooked? Or is there any parameter I need to change to make the meso-simulation
better?
If it indeed is a problem, I can share a solution. Please feel free to contact me via the email below to discuss.
Thank you very much. I look forward to your reply.
--------------------------------
Email:
ying-chuan.ni@xxxxxxxxxxxxxxxx
Traffic Engineering Group (SVT)
Institute for Transport Planning and Systems (IVT)
ETH Zurich
_______________________________________________
sumo-user mailing list
sumo-user@xxxxxxxxxxx
To unsubscribe from this list, visit
https://www.eclipse.org/mailman/listinfo/sumo-user
|


