Typical Language Configurations
Case Insensitive Languages
In some cases, e.g. if your SHIFT key is broken, you might want to design a case insensitive language. Xtext offers options on some of its generator fragments for this purpose.
For case insensitive keywords, open your MWE workflow and enable the ignoreCase property:
... StandardLanguage {
... other config
parserGenerator = {
options = {
ignoreCase = true
}
}
}
For case insensitive element names, use the ignoreCase option in the scoping, too :
scopeProvider = {
ignoreCase = true
}
Whitespace-Aware Languages
Some language designers prefer to use indentation to structure code blocks instead of surrounding them with braces { ... }, which are really hard to type with certain kinds of keyboards. A well-known example of such a language is Python. Another well-known example is the Home Automation language shipped with Xtext, available through File → New → Example → Xtext Examples → Xtext Home Automation Example.
Device Window can be open, closed
Device Heater can be on, off, error
Rule 'Save energy' when Window.open then
fire(Heater.off)
println('Another penny to the piggy bank!')
The 'Save energy' rule contains a code block with two operations, which is indicated by the equal indentation of these operations. Nested blocks are also possible:
Rule 'Report error' when Heater.error then
var String report
do
Thread.sleep(500)
report = HeaterDiagnostic.readError
while (report == null)
println(report)
The first step for including whitespace-aware blocks in your language is to use synthetic tokens in the grammar by writing terminals of the form 'synthetic:<terminal name>':
terminal BEGIN: 'synthetic:BEGIN';
terminal END: 'synthetic:END';
These terminals can be used to mark the boundaries of code blocks. The Xtext Home Automation example inherits expressions from Xbase and redefines the syntax of block expressions:
@Override
XBlockExpression returns xbase::XExpression:
{xbase::XBlockExpression}
BEGIN
(expressions+=XExpressionOrVarDeclaration ';'?)*
END;
After running the workflow, a stub implementation of AbstractIndentationTokenSource is generated in the parser.antlr subpackage, e.g. RuleEngineTokenSource. Here you can specify which terminal rule should be applied to your synthetic tokens. For the Xtext Home Automation language the WS (whitespace) rule is selected, which brings the indentation awareness as seen above.
In case of a whitespace-aware language, the formatter must be either adapted to produce whitespace that correctly reflects the document structure, or it must be deactivated. Otherwise automatic formatting might produce code with different semantics or even syntax errors. See how we customized the formatter in the Xtext Home Automation example.
Languages Independent of JDT
The following section describes how you make your language independent of Eclipse’s Java Development Toolkit (JDT).
In the UIModule of your language you have to overwrite two bindings. First, remove the bindings to components with support for the ‘classpath:’ URI protocol, i.e.
@Override
public Class<? extends IResourceForEditorInputFactory>
bindIResourceForEditorInputFactory() {
return ResourceForIEditorInputFactory.class;
}
@Override
public Class<? extends IResourceSetProvider> bindIResourceSetProvider() {
return SimpleResourceSetProvider.class;
}
Second, configure the global scope provider to scan project root folders instead of the class path of Java projects.
@Override
public Provider<IAllContainersState> provideIAllContainersState() {
return org.eclipse.xtext.ui.shared.Access.getWorkspaceProjectsState();
}
The remaining steps show you how to adapt the project wizard for your language, if you have generated one. The best way to do this is to create a new subclass of the generated IProjectCreator in the src/ folder of the ui project and apply the necessary changes there. First, remove the JDT project configuration by overriding configureProject with an empty body.
The next thing is to redefine the project natures and builders that should be applied to your language projects.
In in this case just remove the JDT stuff in this way:
protected String[] getProjectNatures() {
return new String[] {
"org.eclipse.pde.PluginNature",
"org.eclipse.xtext.ui.shared.xtextNature"
};
}
protected String[] getBuilders() {
return new String[] {
"org.eclipse.pde.ManifestBuilder",
"org.eclipse.pde.SchemaBuilder"
};
}
After that you have to bind the new IProjectCreator
@Override
public Class<? extends IProjectCreator> bindIProjectCreator() {
return JDTFreeMyDslProjectCreator.class;
}
Now your language and its IDE should now no longer depend on JDT.
Parsing Expressions with Xtext
Parsing simple XML-like, structural languages with Xtext is a no-brainer. However, parsing nested expressions is often considered complicated. This is the perception due to their recursive nature and the properties of the parser technology used by Xtext. You have to avoid left recursive parser rules. As the underlying Antlr parser uses a top-down approach it would recurse endlessly if you had a left recursive grammar.
Let’s have a look at parsing a simple arithmetic expression:
2 + 20 * 2
If you know EBNF a bit and wouldn’t think about avoiding left recursion, operator precedence or associativity, you’ld probably write a grammar like this:
Expression :
Expression '+' Expression |
Expression '*' Expression |
INT;
This grammar would be left recursive because the parser reads the grammar top down and left to right and would endlessly call the Expression rule without consuming any characters, i.e. altering the underlying state of the parser. While this kind of grammar can be written for bottom-up parsers, you would still have to deal with operator precedence in addition. That is define that a multiplication has higher precedence than an addition for example.
In Xtext you define the precedence implicitly when left-factoring such a grammar. Left-factoring means you get rid of left recursion by applying a certain idiom, which is described in the following.
Here is a left-factored grammar (not yet working with Xtext) for the expression language above:
Addition :
Multiplication ('+' Multiplication)*;
Multiplication:
NumberLiteral ('*' NumberLiteral)*;
NumberLiteral:
INT;
As you can see the main difference is that it uses three rules instead of one, and if you look a bit closer you see that there’s a certain delegation pattern involved. The rule Addition doesn’t call itself but calls Multiplication instead. The operator precedence is defined by the order of delegation. The later the rule is called the higher is its precedence. This is at least the case for the first two rules which are of a left recursive nature (but we’ve left-factored them now). The last rule is not left recursive which is why you can implement it without applying this pattern.
The next task is to allow users to explicitly adjust precedence by adding parentheses, e.g. write something like (2 + 20) * 2. So let’s add support for that (note that the grammar is still not yet working with Xtext):
Addition :
Multiplication ('+' Multiplication)*;
Multiplication:
Primary ('*' Primary)*;
Primary :
NumberLiteral |
'(' Addition ')';
NumberLiteral:
INT;
Once again: if you have some construct that recurses on the left hand side, you need to put it into the delegation chain according to the operator precedence. The pattern is always the same: the thing that recurses delegates to the rule with the next higher precedence.
Construction of an AST
Now that left recursion is avoided, the parser should produce a proper syntax tree. In Xtext each rule returns a value. Production rules return AST nodes (i.e. instances of EObject), enum rules return enum literals and data type rules as well as terminal rules return simple values like strings. Xtext can automatically infer whether some rule is a production rule, i.e. constructs and returns an AST node, or if it is a data type rule that returns a value. The grammar above only consists of data type rules all of them returning plain strings. In order to construct an AST we need to add assignments and actions to the grammar.
The return type of a rule can be specified explicitly using the returns keyword but can be inferred if the type’s name is the same as the rule’s name. That is
NumberLiteral : ... ;
is a short form of
NumberLiteral returns NumberLiteral : ... ;
However in the case of the expression grammar above, all rules need to return the same type since they are recursive. In order to make the grammar valid, a common return type has to be added explicitly (but the grammar is still missing some bits):
Addition returns Expression:
Multiplication ('+' Multiplication)*;
Multiplication returns Expression:
Primary ('*' Primary)*;
Primary returns Expression:
NumberLiteral |
'(' Addition ')';
NumberLiteral:
INT;
The AST type inference mechanism of Xtext will infer two types: Expression and NumberLiteral. Assignments and actions have to be added to store all the important information in the AST and to create reasonable subtypes for the additive and multiplicative expressions. The fully working Xtext grammar is:
Addition returns Expression:
Multiplication ({Addition.left=current} '+' right=Multiplication)*;
Multiplication returns Expression:
Primary ({Multiplication.left=current} '*' right=Primary)*;
Primary returns Expression:
NumberLiteral |
'(' Addition ')';
NumberLiteral:
value=INT;
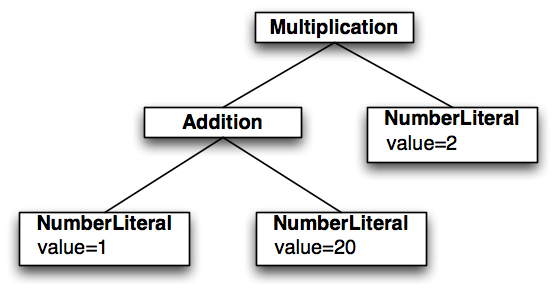
This is how the parser processes the following expression:
(1 + 20) * 2
It always starts with the first rule Addition. Therein the first element is an unassigned rule call to Multiplication which in turn calls Primary. Primary now has two alternatives. The first one is calling NumberLiteral which consists only of one assignment to a feature called ‘value’. The type of ‘value’ has to be compatible to the return type of the INT rule.
But as the first token in the sample expression is an opening parenthesis ‘(‘, the parser will take the second alternative in Primary: it consumes the ‘(‘ and calls the rule Addition. Now the value ‘1’ is the lookahead token and again Addition calls Multiplication and Multiplication calls Primary. This time the parser takes the first alternative because ‘1’ was consumed by the INT rule.
As soon as the parser hits an assignment it checks whether an AST node for the current rule was already created. Otherwise it will create one based on the return type of the current rule, which is NumberLiteral. The Xtext generator created the EClass ‘NumberLiteral’ before which can now be instantiated. That type will also have a property called value of type int, which will get the value ‘1’ set. This is what the Java equivalent looks like:
// value=INT
if (current == null)
current = new NumberLiteral();
current.setValue(ruleINT());
...
Now that the rule has been completed the produced EObject is returned to the calling rule Primary, which in turn returns the object unchanged to its own caller. Within Multiplication the rule Primary has been successfully parsed and returned an instance of NumberLiteral. The remainder of the rule (everything within the parentheses) is a so called group. The asterisk behind the closing parenthesis states that this part can be consumed zero or more times. The first token to consume in this group is the multiplication operator ‘*’. Unfortunately in the current input the next token to accept is the plus sign ‘+’, so the group is not consumed at all and the rule returns the NumberLiteral that was returned from the previous unassigned rule call.
In rule Addition there is a similar group but this time it expects the correct operator. The parser steps into the group. The first element in the group is an assigned action. It will create a new instance of type Addition and assigns what was the to-be-returned object to the feature ‘left’. In Java this would have been something like:
// Multiplication rule call
current = ruleMultiplication();
// {Addition.left=current}
Addition temp = new Addition();
temp.setLeft(current);
current = temp;
...
As a result the rule would now return an instance of Addition which has a NumberLiteral set to its property left. Next up the parser consumes the ‘+’ operator. The operator itself is not stored in the AST because there is an explicit Addition type. It implicitly contains this information. The assignment right=Multiplication calls the rule Multiplication another time and assigns its result object (a NumberLiteral of value=20) to the property right. The closing parenthesis is matched afterwards, consumed and the parser stack is reduced once more.
The parser is now in the rule Multiplication and has the multiplication operator ‘*’ on the lookahead. It steps into the group and applies the action. Finally it calls the Primary rule, produces another instance of NumberLiteral (value=2), assigns it as the ‘right’ operand of the Multiplication and returns the Multiplication to the rule Addition which in turn returns the very same object as there’s nothing left to parse.
The resulting AST looks like this:
Associativity
There is still one topic worth to mention, which is associativity. There is left and right associativity as well as non-associativity. The example above implements left associativity. Associativity tells the parser how to construct the AST when there are two infix operations with the same precedence. The following example is taken from the corresponding wikipedia entry:
Consider the expression a ~ b ~ c. If the operator ~ has left associativity, this expression would be interpreted as (a ~ b) ~ c and evaluated left-to-right. If the operator has right associativity, the expression would be interpreted as a ~ (b ~ c) and evaluated right-to-left. If the operator is non-associative, the expression might be a syntax error, or it might have some special meaning. The most common variant is left associativity:
Addition returns Expression:
Multiplication ({Addition.left=current} '+' right=Multiplication)*;
Right associativity is done using a slightly modified pattern. Note the quantity operator and the call to the rule itself in the group:
Addition returns Expression:
Multiplication ({Addition.left=current} '+' right=Addition)?;
Non-associativity can be implemented in a similar way, but this time the final rule call is not immediately recursive but delegates to the next precedence level:
Addition returns Expression:
Multiplication ({Addition.left=current} '+' right=Multiplication)?;
Sometimes it’s more convenient to allow associativity on parser level, but forbid it later using validation. This allows more descriptive diagnostics. Also the whole parsing process won’t rely on error recovery but the editor will generally be more forgiving.
